The Real-World Data are Multi-faceted

Motivation for interpretable AI/ML models

Why Multi-facet for Complex Data?

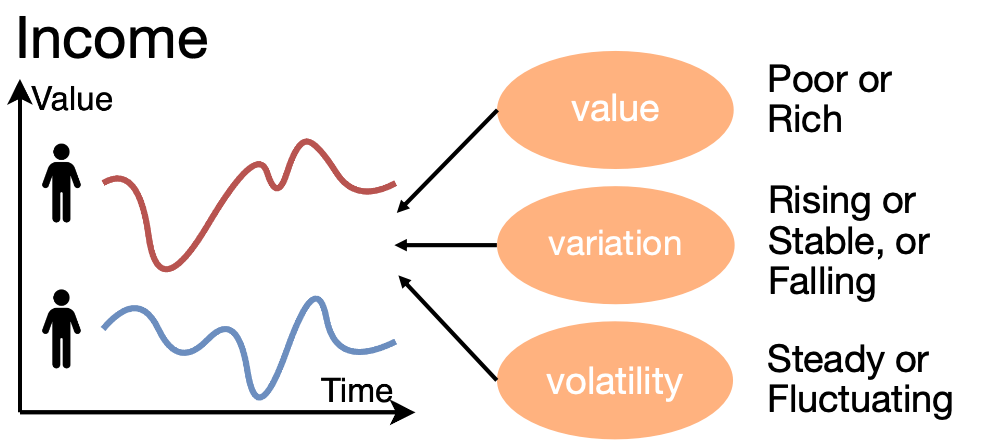
Real-world data are often multi-faceted, particularly when dealing with complex and high-dimensional settings. To illustrate this, we take time series data as an example. In the figure below, the left panel shows individual income trajectories over time, while the right panel presents multiple time series for each person, capturing frailty, wellbeing, and social isolation.

In the case of income trajectories, we might describe a person’s income as “poor, stable but fluctuating”. Such descriptions are determined by three key characteristics of a time series: value, variation, and volatility. In healthcare, however, individuals typically have multiple time series across their lives. The interesting characteristics here could include the intercepts of variables, interactions between variables, the scale of each variable, and the noise in trajectories.

Importantly, these characteristics are not directly observed but are meaningful hidden features that shape the form of an observed trajectory. We refer to each such hidden characteristic as a facet. Within each facet, there can be several specific clusters. For example, in the value facet of income trajectories, clusters might correspond to different levels of income such as “poor”, “comfortable”, or “luxury”. This idea extends beyond time series. Consider an image: if an object is characterized by two facets—shape and color—then the combination of clusters in the shape facet and the color facet allows us to causally and interpretably describe the object’s overall class. This illustrates both the approach and the advantage of considering multiple facets when building AI/ML models.

What Is Multi-facet Clustering?

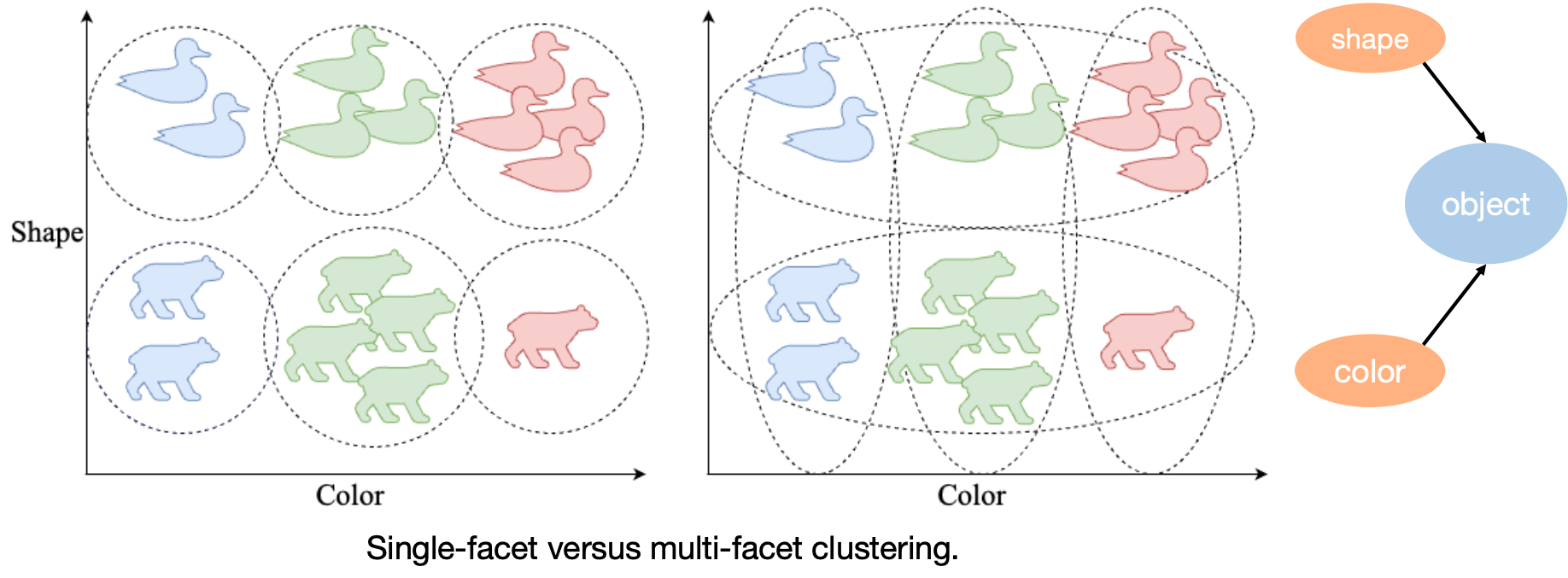
Clustering is widely used in AI applications. However, most traditional clustering methods are what we call single-facet clustering. That is, they partition data by aggregating information from all characteristics/facets. The draw back is that we lose interpretability since we don’t know explicitly which characteristics actually contribute to the clustering solution. By contrast, multi-facet clustering can disentangle these characteristics/facets and partition data along different facets separately and simultaneously.

As illustrated by the following figure comparing single-facet and multi-facet clustering. Suppose each object has two characteristics: color and shape.

This way, each overall cluster can be interpreted in terms of its facet-specific clusters. For more details, we refer to our work on a novel Bayesian multi-facet clustering model for longitudinal data, available here: Wang et al., PMLR 2025.

How Is It Different to Multi-view and Multi-assignment Clustering?

The concept of multi-facet clustering is distinct from Multi-view and Multi-assignment clustering, as shown in the following table. In multi-facet clustering, the input is data from a single cohort, and the outputs are multiple clustering solutions, each corresponding to a different facet. By contrast, in multi-view clustering, the input consists of multiple views of data for the same cohort, but the goal is to produce a single integrated clustering solution that combines all views. In multi-assignment clustering, the input is again data from a single cohort, but the output is a clustering solution on a single facet where each individual can belong to multiple clusters simultaneously.

Method Facet Input Output
Multi-facet Multiple Single data matrix Multiple clusters
Multi-view Multiple Multiple data matrix Single cluster
Multi-assignment Single Single data matrix Multiple clusters